
buarki
FollowSite Reliability Engineer, Software Engineer, coffee addicted, traveler
Supervised Machine Learning: how to build your own Neural Network from scratch
November 16, 2023
4640 views
Share it
Foreword
This article aims to provide a simple, minimalist and baby-steps introduction to how Supervised Machine Learning works. It will explain the underlying idea, the mechanics, and the reasons behind its functionality. Additionally, a concrete and minimalist example with code will be available at the end as a reference. Last, but not least, it does not mean to be a replacement of academic articles on this topic, but an introductory material for the ones who love math and coding.
What is Machine Learning?
In brief, as you can see in this nice article from MIT, "Machine learning is a subfield of artificial intelligence, which is broadly defined as the capability of a machine to imitate intelligent human behavior. Artificial intelligence systems are used to perform complex tasks in a way that is similar to how humans solve problems". We can divide this AI field in three categories: Supervised Learning (and this article will address it), Unsupervised Learning and Reinforcement Learning.
Supervised Learning: an overview
Supervised learning is a branch of machine learning where computers are trained by being presented with examples of desired behavior. It mimics the process of a teacher guiding a student in learning a subject, with continuous checks on the student's progress.
For such type of Machine Learning, the algorithm is trained on a dataset that includes both input data and corresponding correct output or "answers."
A funny example if this is the App "Hot dog and Not hot dog" from the Silicon Valley TV Serie in which the character Jian Yang creates an app able to tell whether or not a picture is from a hot dog or not. For sure that's not the best use case for supervised machine learning, in our day to day life we have much more useful uses like spam filters, product recommendations, fraud detection and so on.
Some methods used in supervised learning include neural networks, naïve bayes, linear regression, logistic regression, random forest, and support vector machine (SVM).
As you can see, even being a subfield of Artificial Intelligence, supervised learning also has its own subtopics. In next section we'll address how supervised learning works using neural networks.
The fundamental pieces of Neural Networks: Neurons and the Universal Approximation Theorem
Dear reader, I must warn you that math is a passion of mine, and I'm thrilled as I write this section. So, proceed at your own risk :)
As previously discussed, supervised learning works by inputting some data into an algorithm and checking if the outcome matches the expected result. When implementing supervised learning using Neural Networks the output computation will be performed as the input passes through the "neurons" of the net. A neuron in this case is essentially a function that receives one or more inputs, such as a vector containing values, does some calculation and provides a result. Each input of such neuron will have a weight attached to it to simulate the synapse process. After summing all (inputs * weights) plus a bias value the neuron applies the result into a activation function which is in charge of introducing non-linearity into the network, enabling it to learn and approximate complex relationships in the data. To help you visualize it check bellow image:
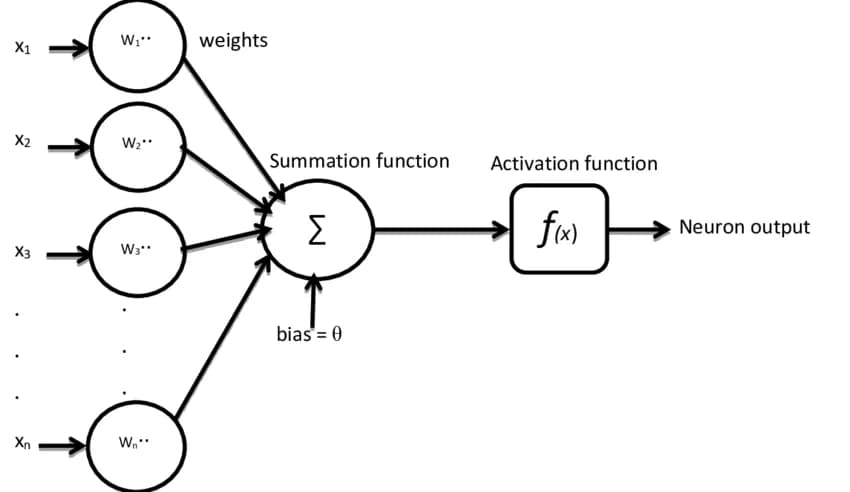
Image took from https://www.researchgate.net/profile/Douw-Boshoff/publication/328733599/figure/fig2/AS:734165188218886@1552050029499/The-structure-of-the-artificial-neuron.png
In above image each "x" represents an input value fed into the neuron and each "w" is a weight applied to an input. The neuron sums all (x*w) with the bias (theta letter) and the output of it is applied into the f(x). Mathematically we can describe it as the following:

Where yk is the output of the kith neuron and f is an activation function, for instance it could be a sigmoid function. Above equation is enough to explain how a neuron works, but it is doesn't explain why it works.
To grasp why it operates, let's revisit the fundamental concept of supervised learning: we possess a labeled dataset that serves as the training data for a Neural Network, allowing it to comprehend the underlying patterns. Consider the following example: we aim to create a function, denoted as f(x), which, based on the hours of study by a computer science student, predicts their linear algebra test score. We assume that the student has already taken three tests, and we have their corresponding scores:
| Hours of Study | Score |
|---|---|
| 6 | 8 |
| 7 | 7 |
| 7 | 8 |
Generalizing the idea we get:
| Hours of Study (x) | Score (y) |
|---|---|
| x0 | y0 |
| x1 | y1 |
| x2 | y2 |
| ... | ... |
| xn | yn |
Thus, our job here is to find a function f(x) so that: f(xi) is very close to yi, where i = 0,1,2...n. To do so we define a family of functions F that could be a good fit for this problem, like linear regression:

If, and only if, there really exists a function that could represent the relation between xi and yi we can take this as an approximation problem: how can we find an element from F as close as possible from our desired function?
We don't all have corresponding yi for all xi, only a few samples where for sure f(xi) = yi. Thus, the best we can do is find a function that properly fits the relation between xi and yi, generalize unknown examples and is computationally possible to find. In other words, we want an element from F that minimizes the supremum norm:

The best approximation.

The supremum norm.
As we want the best fit between input data and output as possible we need to find the minimal ||f - u||. The supremum norm is a mathematical tool that helps us measure the maximum vertical distance between the true function and our approximation across all possible x values. By minimizing this supremum norm, we seek a function within F that provides the closest possible approximation to our desired function.
A proof that the mathematical Neuron definition I've shown above is capable of finding the minimal ||f - u|| is given by the Universal Approximation Theory (UAT), and this quick video shows why Neural Networks are able to learn pretty much any function due to the UAT.
The overall process is defining a small ε value that will control how closely the elements of F will fit our model. The smaller ε is more accurate our Neural Network will be. Once ε is defined we start searching a Neural Network in which the outputs are close to our desired f, bellow image (tries) to show it:

Neural Network trying to fit the model.
Although the UAT proves that such function u(x) (an element of F) exists it doesn't tell us how to find it and the required amount of neurons needed to fit f(x) might be really big, due to that finding an optimal Neural Netwok in practice is a challenge. Besides of it there are other points to take care while chasing for a Neural Network, such as avoiding overfitting and underfitting, the quantity and quality of data required, computational resources available and so on.
Such challenges will be addressed in next section, by assessing a simple problem as example and showing one possible way to find an optimal approximation (a Neural Network that fits the behavior of an f).
Defining a concrete problem as example to solve and planning data architecture
We want to create a model that based on the amount of hours of study and the amount of hours of meditation of a computer science student we find its linear algebra test score. We can also assume that the student has already attempted to perform three tests and we have their respective score:
| Hours of Sleep | Hours of Meditation | Score |
|---|---|---|
| 6 | 5 | 8 |
| 7 | 4 | 7 |
| 7 | 5 | 8 |
If we assume that the model we are trying to create is a function, then the hours of sleep and hours of meditation are inputs of such function, while score is the output. Let's define the vector X as the input of our model and Y as the output of it. Just to clarify it, if f(x) represents our Neural Net and one possible input is X=[6,5] (where 6 is the hours sleept and 5 hours of medidation) then f(X)=[8] (where 8 is the test score). The same way would be if X=[7,4] and f(X)=[7] and also if X=[7,5] and f(X) = [8]. A clever way to approach how we group inputs and outputs would be using matrices of them, then we would have the input matrix:

Matrix with the Neural Network inputs.
Each line on above matrix X is a valid input where the left column represents the hours of sleep and the right column the hours of meditation. And then f(X) will be:

Matrix with the Neural Network outputs.
Each line on above matrix Y is a valid output of the Neural Network.
One thing that must be pointed is that both matrices data must be scaled to ensure that the Neural Network handles standardized units. One way to achieve it is using Min-max normalization.
With the problem stated and input features known we can plan how the Neural Network structure will be. As our input data has two dimensions we need an input layer with two inputs, and as our result is a single number our network has one output only. Thus, the basic structure required for our Neural Network is the following:

The basic structure of our Neural Network.
To complete the structure we need to plan the hidden layers of it. The amount of inner layers may vary depending on the problem the Neural Network needs to solve. In fact, real world examples could have millions of hidden layers. For the sake of simplicity we'll stick if one hidden layers with 3 neurons only, and bellow image image shows it:

The completed structure of our Neural Network.
Some important things missing on image above are the neuron weights. We will assume that the weights of first layer are always 1 and ignore them, so applying them on the second and third layer we get:

The completed structure of our Neural Network with Neuron weights.
In case you didn't get the weight notation take a look at bellow image:

The completed structure of our Neural Network with Neuron weights.
In next section we will properly address how the Neural Network model is built based on this proposed structure.
The Neural Network model in action: forward process
The process of acctually using the Neural Network is called forward process. Here the Neural Network receive the inputs, pass all of them through the weights, apply the sum into the activation function and proceed to next layer.
Let's start checking how the process works on the second layer. Each neuron inside of second layer will receive the input from all neurons from first layer and apply a weight on it. Once all inputs are weighted we will get the following:

Neural Network with all second layer's input weighted.
Considering that we placed all input values into the matrix X and it is a 3x2 matrix, if we place all weights also on a matrix 2x3 we will end up having a matrix containing the results of all (inputs * weights). Let the weight matrix of second layer be:

Matrix with second layer weights.
Then, the product:

Will be:

We'll call the above product as:

Even before you ask: we'll address the bias in next sections.
Once we calculated the weighted sum for each neuron we can now apply the activation function element wise on above matrix to calculate the output of second layer. For this problem, the activation function used will be the sigmoid:

Sigmoid activation function.
Thus, the second layer output can be defined as:

Matrix containing second layer output.
Once second layer is finished we proceed to the third layer with exact same process and with the second layer output being the third layer input. Let's start by seeing the third layer weights:

Matrix with third layer weights.
Multiplying the second layer output with third layer weights will gives us:

And to get the output of third layer we apply the sigmoid on this product:

Matrix containing third layer output.
Above matrix has shape 3x1 and each line represents the predicted test score.
With the equations discussed in this section we are able to predict the test score based on the amount of study and medidation hours. But such predictions will probably be absolutely wrong :). This is due to the fact that the weights from our layers once we create the Neural Network are defined randomly. Thus, the Neural Network won't be useful on helping us predicting the test score. To adjust the Neural Network we need a way to find proper values for our weights while we measure the accuracy of outputs. This will be addressed in next section.
Assessing the Neural Network error: error cost
In order to improve the Neural Network accuracy we need to know how wrong the outputs are. To do so we'll use a cost function (or loss function). The cost function will measure the performance of our machine learning model quantifying the error between the prediction and expected value. A good way to address the cost function is using the Mean Squared Error (MSE) (soon it will be explained why such approach is effective and smart). In mathematical terms we can define MSE by the following:

The error of our Neural Net.
On above equation, E is the global error of our Neural Network, y' is the expected output for one input and y is the received output for one input. In the case you are wondering why we placed the term 1/2: it was done for convenience during derivatives operations as it simplifies the computation of gradients and it doesn't alter the fundamental meaning of Mean Squared Error (MSE), which remains a measure of the average squared difference between predicted and actual values.
Being brief, training a Neural Network means minimize its cost function. Our cost function is a function of the Neural Network input and its weights, and in case this is not clear we can expand E:

Expanding the Neural Network error cost.
We just don't have control over the X param, only the "client" of the Neural Network does. Thus, if there is something we can change in order to adjust the cost function is the Neural Network weights. But how can we adjust the weights? Brute force?
If we consider for a while a hypothetical Neural Network containing one weight only in which the "proper" value for it can be found on a set of 10k numbers, a brute force approach would take in the worst case 10k "checks" to find the proper values. If we also assume that each "check" takes 2 milliseconds (ms), then, the overall process would take 20 seconds. Anoying but still feasible.

How the error cost would look like for one neuron.
It would takes us 10k times executing the forward process, calculating the error cost to, in the end, find the minimal error value. If we expand it to two neurons and we assume that this new neuron also has the proper value on a search space of 10k numbers, in such scenario, our search would require 100000000 iterations (10k * 10k), and if we also keep the check time of 2ms it would take 200,000 seconds or approximately 56 hours :)

How the error cost would look like for two neurons.
The conclusion here is obvious: the more neurons the Neural Network has, more expensive its training will be. This phenomenon is called Curse of dimensionality, which is a serie of challenges and issues that arise when dealing with data in high-dimensional spaces.
As we could see, bruce force solutions are not feasible here. We need a way to find a shortcut between all the available numbers in the search space to the ones that gives us the minumum of error cost function. We could achieve it by kwnowing the direction that E decreases from one inspected point. Let's consider the scenarion with one single neuron again to visualize it. Consider bellow image where point P(wi, E(wi)) is a known point in the availble search space and we know that moving to the right decreases E while moving to the left increases E. Then, as we want to minimize E we can move to the right.

We can extend this ideia by asking: how E behaves when the weights changes? And fortunely there is an awesome tool to helps us finding it out called calculus, specifically the the derivatives. As mentioned above, E is a function of both Neural Network inputs and the weights, but we control only the weights. Thus, to know how E behaves by modifying weights we need to calculate the derivative of E with respect of the weights. If derivative of E with respect to the weights is positive we can say that E is increasing, otherwise it is decreasing. For the case of our Neural Network, which has more than one layer, we need to perform a parcial derivative of E with respect to each layer weight.
By knowing the direction that E decreases we can iteratively look for lower values of E, ignoring points where it increases optmizing the search time. Check bellow image to visualize it:

A clever way to find lower values of E.
The method described above is called Gradient Descent, which is a way to minimize the cost function by adjusting the model params in such a way that the cost decreases faster. It works by calculating the gradient (slope) of the cost function with respect to the parameters and updating them in the opposite direction of the gradient, moving towards the minimum of the cost function. We basically repeat this process until the cost function reaches the minimal value.
An important thing to point is that we can use Gradient Descent for our Neural Network because our error cost function has a convex shape, which ensures that E always moves on "the same direction". The convex shape is a consequence of using the MSE, which is a quadratic function :)
If our cost function didn't have such convex shape it could mess our Gradient Descent execution, and our search could end up being stuck on a local minimum rather than the global minimum. Check bellow image:

Showing the problem of local and global minimum.
It also worth poiting that for some scenarios the shape of cost function doesn't matter, for instance in the case of using Stochastic Gradient Descent, where you use one input example at time. In our case we'll be using Batch Gradient Descent, where rather than one training example at time we'll use a set of it.
Backpropagation: adjusting weights using Gradient Descent
To perform the Batch Gradient Descent process to update the Neural Network weights we need to calculate the partial derivative of E with respect to our weights from second and third layer. Let's start with third layer.

As the derivative of a sum is the sum of derivatives we can move the inner sum to the outside:

For simplicity, let's remove the outter sum and focus on the derivative part of an isolated case. That said, if we apply the chain rule we would get:

As the term y' is the expected output then it is a constant. Resolving the equation we get:

If we remember that y (the output of Neural Network) is the result of the activation function applied on v(3) and apply the chain rule again we get:

The derivative of second term is the derivative of our activation function S, which is a sigmoid. The derivative of S is:

Applying it we get:

This part is a little bit tricky due to matrix dimensions, but don't give up :)
A few iterations ago we have removed the Σ from our calculations to look to the problem isolatedly and now we can go back to it. Both matrices y' and y have same dimentionality and the subctration between them can occur without any problem. The interesting part is what to do with S', as it has the same dimension of the matrix subtraction. If we look closely on how this product would happen if we were applying the Σ summation we could see that this multiplication would be done element-wise. Thus, to represent it in the form of matrices mutiplication we can use the Hadamard Product. Adding the proper notation to it we get:

The last derivative to solve is the third term, which result is the Y(2). As in this step we are propagating the error backwards to the weight that generated it we need to mutiply the elements of Y(2) to its proper back propagating error. We can do so by multiplying the transpose of Y(2) by the first two terms:

And we are done with third layer! Proceeding to the second layer, the overall process is the same, the difference is that now we'll perform the derivative of E with respect to W(2). We can start with:

Solving it we'll have:

Applying the chain rule we get:

The first two terms are already known:

And if we keep applying the chain rule:

If we reorganize some terms on above equation and also on the one for the third layer we'll see they have a product in common:

This product is the back propagating error of third layer. We can add the following notation to it:

We can rewrite the equation for second layer to be the following:

If we extend the idea, we can also define the back propagating error to the second layer and we'll have the following:

Once we finished the equations for both second and third layer we are able to adjust the Neural Network weights by subtracting them with each respective gradient component. We need to subtract because the gradient points in the direction of the steepest increase of the error, to reduce the error we need to move in the opposite direction of the gradient. Thus, by subtracting we are adjusting the weights in the direction that decreases the error.
We can also mutiply our gradient component for a small scalar to control the size of the steps taken during each iteration of the optimization process. This scalar is useful because it controls the size of the weight adjustments, ensuring that the optimization process is stable and converges to a meaningful solution. This scalar is often called learning rate. Finding a proper learning rate is important because a too-large learning rate can cause the optimization process to oscillate or diverge, potentially missing the minimum. On the other hand, a too-small learning rate can make the convergence very slow, requiring many iterations to reach the minimum. By doing some researches we can find some suggestions on how to configure out the learning rate, one common suggestion is something between 0.01 and 1.0 .
Thus, to update weights matrices we do the following:

Where α is the learning rate. One thing worth point specifically during the implementation of such step is to test the implementation to ensure it was well done. Any implementation glitch on this step would lead to wrong Neural Network results and problems very hard to debug :)
Training the Neural Network
Once we have designed the Neural Network structure, planned its forward process and the backpropagation process we are able to effectively train it. The idea is pretty simple: we define a param to controll how many "iterations" the training will have, usually this param is called epoch, and also the already mentioned learning rate. The learning rate, the amount of epochs and the number of layers are examples of what we call hyperparameters. Once we define such numbers the process goes like: for each epoch, execute the forward process, compute the error between the expected values and received values, calculate the gradient descent and update the weights. A very high level algorithm would be:

With a reasonable amount of data with proper quality, time and computer power, above process will do the job, but there are some pitfalls during such process, specially for Neural Networks with a much bigger number of layers. For instance, finding a proper learning rate is a non trivial task and a bad weights initialization can result slow convergence or even convergence to suboptimal solutions. There are alternatives that can be explored such as BFGS technique, as it can perform a faster convergence and does not requires a manual definition of the learning rate.
Now we are missing to address two points to complete our basic knowledge about Neural Networks: bias and regularization. We'll discuss them in next sections.
Bias: enhancing flexibility
One component that so far we skipped is the bias on Neural Networks. An important job it does is giving to the Neural Network the hability to learn different constants for each neuron, which is crucial for fitting diverse patterns in the data. It also helps Neural Networks to model nonlinear relationships. Moreover, it allows neurons to be "activated" even when the weighted sum of inputs is below zero, and this is important for modeling situations where certain features may not contribute much to the output individually but still play a role when combined with other features.
In order to introduce the use of bias in our model we might need to adjust the found equations a little bit. The first adjustment is on how we calculate the weighted input, now we need to add a matrix B containing the biases:

And we also need to update B(2) and B(3) during the backpropagation. The ideia is the same applied to weights, so if we start with B(3):

And to update B(3) we do:

For B(2) we also do the same process, and due to that we can ommit some parts:

And to update it:

Now we can finally move to last step :)
Overfitting: we can't ignore the noise!
Let's assume that in a few days the same student will have another linear algebra test, and it is hopping to pass it now :). So the student uses our Neural Network to find a proper combination of hours of study and meditation to succeed on the test. It concludes that a score 7 is enough and testing based on the vector X=[7,4], which also is record from its previous test, it decides to study for 7 hours and medidate for 4. Once the test score is informed it sees it scored 5 :(
There can be several reasons for the model predict such wrong score, like the student missing to review a topic in which the test focused more, the student having headache during the test, or even back luck.
The important point here is the data we use to design our model is just a perception of a fact, but between the fact per se and our observation there is noise. In other words, there are other factors that influence the test score, and some of them we might not even be aware that they exist. If a model doesn't take it into account the Neural Network can endup having overfitting issues, which is when the Neural Network performs good with training data but badly with unseen data.
Overfitting verification is a must have during the Neural Network training and one interesting way to do so is split the training data in two parts: a bigger one to train the Neural Network while iterating through some epochs, and a smaller one to evaluate if the training caused an overfitting.
To avoid having such problems we can introduce a form of regularization that will discourage overly complex models with excessively large parameter values. Common regularization techniques are Ridge and Lasso regularization, in our approach we'll use the Ridge method. To do so we need to adjust how we calculate the error cost E and the gradient components. For the error cost we can do:

On above equation, the right added term can be interpreted as a penalty for complex models. The β is a regularization hyperparameter that helps us to control the relative cost. Higher β implies in bigger penalties for higher model complexity, resulting in less overfitting. We also are multiplying the left term by 1/n where n is the amout of input samples, thus the number of rows of X. This term is important as it ensures that the regularization penalty is not overly influenced by the size of the dataset. The regularization term involves summing up the squared weights across all parameters. Without normalization, this sum would grow with the number of examples in your dataset. By dividing by the number of examples we ensure that the regularization term is on a consistent scale, regardless of the size of your dataset. If we don't normalize it, the regularization term might dominate the loss term in the objective function, especially for large datasets. This could lead to the optimization process being overly sensitive to the regularization term, potentially overshadowing the impact of the actual loss term.
About the gradient components we can do:

And that's it :)
Summary
We went through a lot of points in deep details, so let's wrap it up like a check list of "what to take care while creating a neural network to solve a supervised machine learning problem".
1. Understand the problem
- - What is the problem we are trying to solve?
- - What are the inputs of the model we need to create?
- - What are the outputs of the model we need to create?
2. Neural Network topology
- - How many dimensions our input layer requires?
- - How many dimensions our output layer requires?
- - Which hyperparameters needs initialization?
- - How do we initialize weights? Random values?
- - How do we initialize biases? Random values?
3. Training data
- - Which amount of data do we need to train the model?
- - Does the training dataset requires cleaning?
- - How much of the dataset will be used for training and how much to check the training?
- - How can we check if we have overfitting problems?
Reference Code
I put a minimalist implementation of a Neural Network to solve the problem of the student trying to pass the linear algebra test, you can see the code on my Github repository.
Key References
- Approximation by Superpositions of a Sigmoidal Function; G. Cybenkot.
- The Universal Approximation Theorem; Alexander.
- Machine learning, explained; Sara Brown.